Module 0013: Conditions and conditional statements

About this module

Why?

Conditional statements are important because they permit a program to follow different paths based on the outcome of conditions. In other words, conditional statements give programs the ability to “choose”.

Conditions

A condition is essentially a question that can only have one of two answers: “true” or “false”. I choose to use “true” and “false” instead of “yes” and “no” for a reason. Let us examine this question:

Is variable x greater than variable y?

Obviously, the answer is either “yes” or “no”. However, let me change the question just a little, as follows:

Is variable x not greater than variable y?

Although the proper answer is still either “yes” or “no”, it depends greatly on the (natural) language. In English, for example, if x > y, then the proper answer to “Is variable x not greater than y?” is “yes”. However, in some other languages, the proper answer is “no”. This is why “yes” and “no” are not really good answers.

As a result, it is better to pose questions as follows:

Is it true or false that x > y?

We can now flip the question as follows: Is it true or false that x is not greater than y?

It is important to remember that in programming, x > y is not an assertion; it is a question. That is, x > y is not saying that x is actually greater than y, but rather asking the question “is it true that x is greater than y”. This means that x > y in programming should have been x ?>? y, just to make it clear.

Comparisons

The first and more primitive kind of condition consists of the comparison operators. This is a list of comparison operators that exist in all programming languages:

It is important to distinguish = from == in a C-derived language. This topic is out of scope in this module. However, it suffices to say that this is a source of many defects in programming.

These comparison operators take two values, one on each side of the operators.

Logical operators

Although comparison operators are useful, they cannot express all the conditions that a program requires. However, we’ll get back to this topic later.

Conditional statements

Let’s try to express the logic to compute the maximum of two variables, x and y, and put that maximum value in variable z. This kind of logic cannot be expressed by sequential statements because whether z should receive the value of x or the value of y depends on the relationship of x and y.

I think we have enough suspense already. The proper code for this logic is as follows:

// algorithm findmax2
if (x > y) // line 1
  z = x;   // line 2
else       // line 3
  z = y;   // line 4

Line 1 expresses the question of whether x is greater than y. Line 2 is the statement that executes if and only if x is actually greater than y (X > y is true). Line 4 is the statement that executes if and only if x is not actually greater than y (x > y is false). Line 3 is merely a separator marker to separate the statement groups. Line

Also, note that the statements on line 2 and line 4 are “indented”. This means that they are shifted a little to the right-hand side. The purpose of indentation is to indicate how a statement “embeds” another one. This will become more important later.

A conditional statement is also graphically presented as follows:

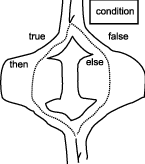
If-then-else template

Note that this is not a flowchart but rather a “trail map.” There is no special symbol to remember! In this picture, the condition is a question of a post before entering the fork. One path of the fork is chosen based on the answer to the question (on the post). If the answer is “true,” then the left path is chosen. If the answer is “false,” then the right path is chosen. The bubble on the left-hand side is labeled “then”; it represents whatever needs to be done if the answer is “true.” Likewise, the bubble on the right-hand side is labeled “else”; it represents whatever needs to be done if the answer is “false.”

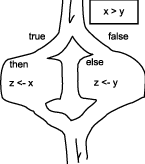
Given this template, we can substitute the proper condition and actions for algorithm findmax2. The resulting trail map is presented as follows:

The pictorial representation of algorithm findmax2

In practice, it is difficult to draw trail maps. Instead, flowcharts are used. The following is a flowchart that represents the same logic as the above trail map.

flowchart TD
start@{shape: terminal, label: "start"}
cond@{shape: diamond, label: "x > y"}
start --> cond
thenStmt@{shape: rect, label: "z = x"}
cond -->| true | thenStmt
cond -->| false | elseStmt
elseStmt@{shape: rect, label: "z = y"}
end1@{shape: diamond, label: " "}
end2@{shape: terminal, label: "end"}
thenStmt --> end1
elseStmt --> end1
end1 --> end2

The syntax of a conditional statement

condStmt is a conditional statement. condition is a condition, which is also known as an expression that evaluates to true or false. thenStmt is the “then statement,” it executes if and only if *condition* is true. elsePart is an optional part of specifying an else statement. elseStmt is the “else statement,” it executes if and only if condition is false.

The last rule specifies that a statement can expand to a condStmt (conditional statement).

Logical operators

Although comparison operators are important and useful, they are not sufficient to express all the different kinds of conditions needed in programming. Let us think about the logic to figure out the maximum z of three variables w, x and y.

We know that we need to rely on a conditional statement. In fact, we can guess the overall form of the statement (in algorithm template findmax3).

// algorithm findmax3 template
if (_c1_)      // line 1
  z = w;       // line 2
else if (_c2_) // line 3
  z = x;       // line 4
else           // line 5
  z = y;       // line 6

The notations _c1_ on line 1 and _c2_ are placeholders for two conditions that we need to figure out. Line 2 should execute if and only if w is the maximum. Similar logic applies to lines 4 and 5. Let us focus on line 2 for now.

How can we confirm that w is the maximum? If w >= x and w >= y, then by definition, w is the maximum. But how do we express this as _c1_?

The syntax to do this is (w >= x) && (w >= y). The symbol && means “and,” also known as “conjunction” in mathematics.

How to say “true” and “false”

In C++, the literal constant value to specify true is simply true as a terminal. Similarly, false is the terminal to specify the value of false.

Any value that is true or false is also known as a boolean value.

Conjunction

“Conjunction” is an operator that has two sides. The entire expression is true if and only if both sides are true. In English, a conjunction is “and”. In C and other C-derived languages, the conjunction operator is &&. In Pascal, SQL, and Visual Basic, the operator is simply spelled as AND.

The four possible combinations are as follows:

This can also be summarized in a truth table as follows:

x y x && y
false false false
false true false
true false false
true true true

In this table, x and y are independent variables, meaning their values do not depend on each other. Each row of the table shows the value of the boolean expression x && y given the values of x and y specified on the same row.

Disjunction

Disjunction is the English word “or”. This operator also requires two sides. The entire disjunction expression is true if and only if at least one side is true. In C and other C-derived languages, the disjunction operator is ||. In Pascal, SQL, and Visual Basic, the operator is simply spelled as OR.

The four possible combinations are as follows:

This can also be summarized in a truth table as follows:

x y x || y
false false false
false true true
true false true
true true true

Negation

Negation is the English word “not”. This operator only has one side (on the right-hand side). A negation expression is true if and only if the value of the right-hand side is false. In C and other C-derived languages, the operator is ! (exclamation point). In Pascal, SQL, and Visual Basic, the operator is spelled out as NOT.

The two possible combinations are as follows:

This can also be summarized in a truth table as follows:

x !x
false true
true false

Back to the example

Getting back to the example to compute the maximum of three variables, we can now utilize the conjunction operator as in the following code.

// algorithm findmax3
if ((w >= x) && (w >= y))      // line 1
  z = w;                       // line 2
else if ((x >= w) && (x >= y)) // line 3
  z = x;                       // line 4
else                           // line 5
  z = y;                       // line 6

The corresponding flowchart is as follows:

flowchart TD
start@{shape: terminal, label: "start"}
cond1@{shape: diamond, label: "w >= x && w >= y"}
cond2@{shape: diamond, label: "x >= w && x >= y"}
start --> cond1
thenStmt1@{shape: rect, label: "z = w"}
cond1 -->| true | thenStmt1
cond1 -->| false | cond2
cond2 --> | true | elseThenStmt
cond2 --> | false | elseElseStmt
elseElseStmt@{shape: rect, label: "z = y"}
elseThenStmt@{shape: rect, label: "z = x"}
end3@{shape: diamond, label: " "}
elseThenStmt --> end3
elseElseStmt --> end3
end1@{shape: diamond, label: " "}
end2@{shape: terminal, label: "end"}
thenStmt1 --> end1
end3 --> end1
end1 --> end2

Now that the algorithm is finished, let us try to trace it. In our first example, let us assume w==2, x==2 and `y==2. Although this is a trivial case, a trace of the algorithm illustrates a conditional statement with multiple conditions.

line # w x y z comments
pre 2 2 2 ? z has an unknown value
1         2 >= 2 is true, the condition is true
2       2 z is updated by w
post          

This example illustrates one very important point. In a complex conditional statement, even though multiple conditions may be true, only the statement matching the first (in top-to-bottom order) true condition executes.

Now, it is your turn to work out the next example. Assume w==2, x==3, and y==3. Create a trace table that shows exactly which lines get executed.

What is “Else if”?

In algorithm findmax3, we use a construct that was not present in algorithm findmax2. What exactly is “else if”?

Let us rewrite algorithm findmax3 in a slightly different format.

// algorithm findmax3
if ((w >= x) && (w >= y))      // line 1
  z = w;                       // line 2
else                           // line 3
  if ((x >= w) && (x >= y))    // line 4
    z = x;                     // line 5
  else                         // line 6
    z = y;                     // line 7

Most programming languages like C++ and Java ignore indentations and how a program is broken into lines. This new way to express findmax3 is functionally identical to the earlier one. However, the indentations in this newer version are structurally correct. There are two conditional statements; one is nested within the other. Technically, the following flowchart represents the nested nature of this code.

flowchart TD
start@{shape: terminal, label: "start"}
cond1@{shape: diamond, label: "w >= x && w >= y"}
cond2@{shape: diamond, label: "x >= w && x >= y"}
start --> cond1
thenStmt1@{shape: rect, label: "z = w"}
cond1 -->| true | thenStmt1
cond1 -->| false | elseBlock
subgraph elseBlock
start2@{shape: terminal, label: "start"}
start2-->cond2
cond2 --> | true | elseThenStmt
cond2 --> | false | elseElseStmt
elseElseStmt@{shape: rect, label: "z = y"}
elseThenStmt@{shape: rect, label: "z = x"}
end3@{shape: diamond, label: " "}
elseThenStmt --> end3
elseElseStmt --> end3
end4@{shape: terminal, comment: "end"}
end3-->end4
end
end1@{shape: diamond, label: " "}
end2@{shape: terminal, label: "end"}
thenStmt1 --> end1
elseBlock --> end1
end1 --> end2

The following is an over-simplified syntax analysis of algorithm findmax3. Note how one conditional statement is the elseStmt of another.

flowchart TD
if1[if]
op1["("]
cond1["(w >= x) && (w >= y)"]
cp1[")"]
condition1(condition)
condition2(condition)
zGetsW[z = w;]
stmt1(thenStmt)
stmt2(thenStmt)
stmt3(elseStmt)
stmt4(condStmt)
stmt5(condStmt)
stmt6(elseStmt)
elsePart1(elsePart)
elsePart2(elsePart)
stmt5 -.-> stmt6
else1[else]
if2[if]
op2["("]
cond2["(x >= w) && (x >= y)"]
cond2 -.-> condition2
cp2[")"]
zGetsX[z = x;]
zGetsX -.-> stmt2
else2[else]
zGetsY[z = y;]
if1 --> op1
op1 --> cond1
cond1 --> cp1
cp1 --> zGetsW
zGetsW --> else1
zGetsW -.-> stmt1
else1 --> if2
else1 -.-> elsePart1
if2 --> op2
op2 --> cond2
cond2 --> cp2
cp2 --> zGetsX
zGetsX --> else2
zGetsX -.-> stmt2
else2 --> zGetsY
zGetsY -.-> stmt3
if1 -.-> stmt4
op1 -.-> stmt4
cond1 -.-> condition1
condition1 -.-> stmt4
cp1 -.-> stmt4
stmt1 -.-> stmt4
stmt6 -.-> elsePart1
elsePart1 -.-> stmt4
if2 -.-> stmt5
op2 -.-> stmt5
condition2 -.-> stmt5
cp2 -.-> stmt5
stmt2 -.-> stmt5
else2 -.-> elsePart2
stmt3 -.-> elsePart2
elsePart2 -.-> stmt5
This site is licensed under Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International 🅭🅯🄏🄎.
Improve this page by contributing and editing ,
or create an issue or participate in a discussion.
or View the source document.